200以上 三角関数 角度の求め方 110731-三角関数 角度の求め方 公式
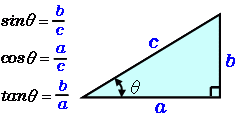
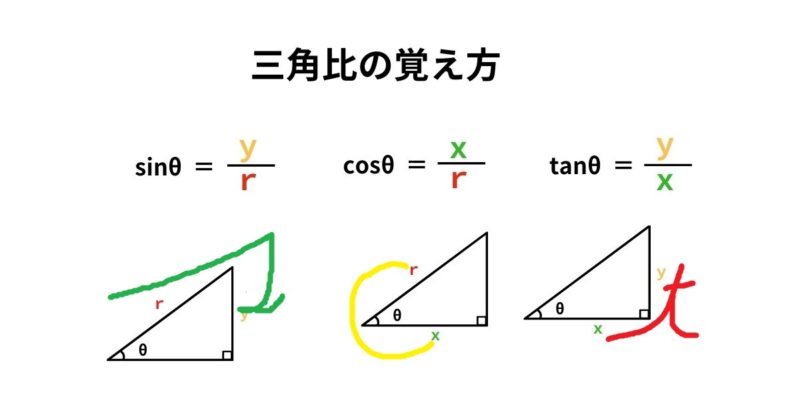
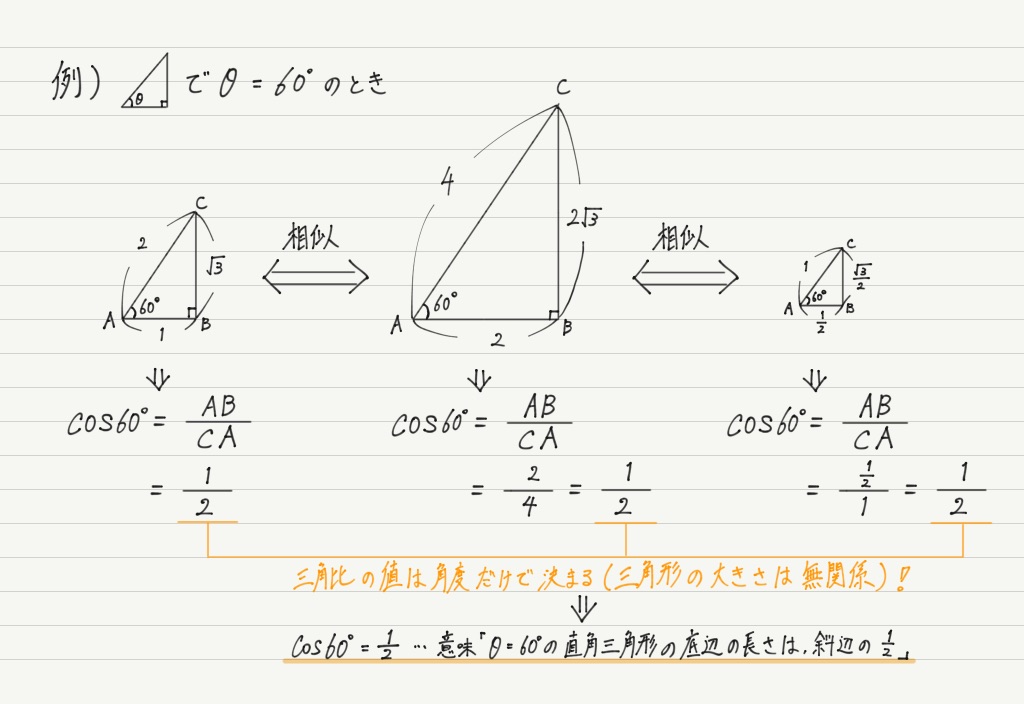
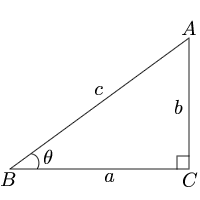
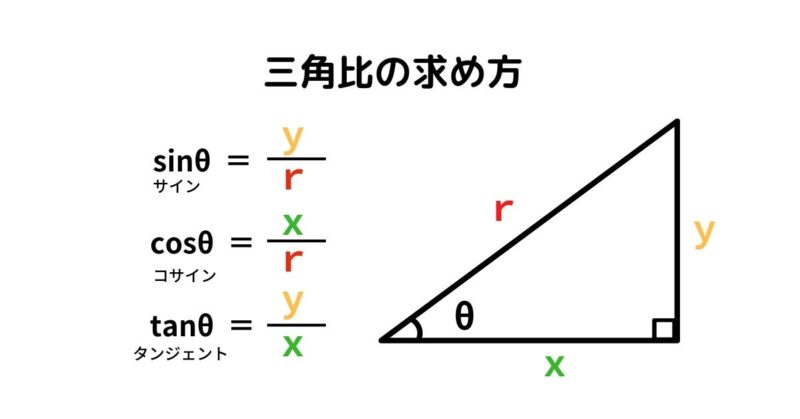
動径 が 軸の正の向きをなす角度を とするとき,次の比の値は(相似図形の性質から)半径 の大きさに関係なく,角度 だけで定まる.そこで, の関数になり,三角関数と呼ばれる. ( 日本語 正弦 せいげん , 読み方 サイン )/ 三角関数(度) 答えの度分秒(° ′ ″ )は、秒の小数点以下2桁まで求めています。 Right triangle (1) cosθ = a c, sinθ= b c, tanθ= b a (2) P ythagorean theorem a2b2 =c2 R 三角比の値の求め方数学苦手な人に向けて基本をイチから解説していくぞ! 余弦定理の公式覚え方はどうする?角度の求め方などを解説! 二次関数係数の符号の決定、グラフから符号を決めるポイントを解説!
2点間の距離を測ろう 三角関数 Gameworks Lab
三角関数 角度の求め方 公式
三角関数 角度の求め方 公式-この問題を見て,逆三角関数 tan1 (C言語では atan() や atan2()) を使って CP と CQ の角度をそれぞれ求め, 両者を比較しようと考えた方が多いのではないでしょうか. しかしこの問題では,角度そのものではなく角度差の符号を求めればよいので, 逆三角関数を使う方法よりも簡単で優れた,外積 高校で習う三角関数ですが、当然数学検定でも前提知識として求められます。 三角関数の基本となる、 sin 、 cos 、 tan に関しては求め方と意味をまずは理解しましょう。 そうする事で後々出てくる公式の意味や求め方もスムーズに理解出来るようになります。



角度 の 求め 方 ニュース ニュース
使用方法は=tan(ラジアン表記での角度)と入力します。 Enterを押して、タンジェントの数値を求めていきましょう。 以下のように基準となるセルを計算します。 後は、 オートフィル機能 で一気にtanの数値を算出していきましょう。 このように三角関数さを求めたい 「=11*SIN(RADIANS (36))」と入力 三角関数とは逆に「辺の長さから角度を求める」には、逆三角関数を使い ます。 逆三角関数にはアークサイン(arcsin、逆正弦)、アークコサイン この角度を $\theta$ とおくと、タンジェントの定義より直角三角形の高 直角三角形の高さを求めるための式 さを求めたい 「=11*SIN(RADIANS (36))」と入力 三角関数とは逆に「辺の長さから角度を求める」には、逆三角関数を使い ます。逆三角関数にはアークサイン(arcsin、逆正弦)、アークコサイン
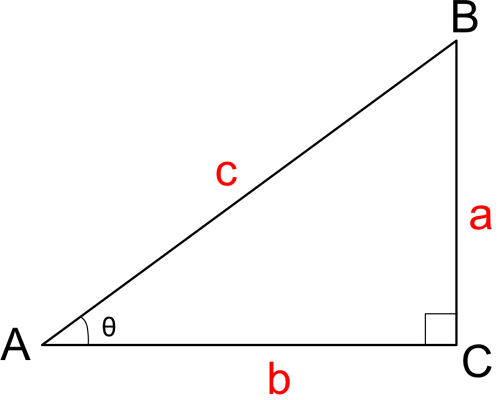
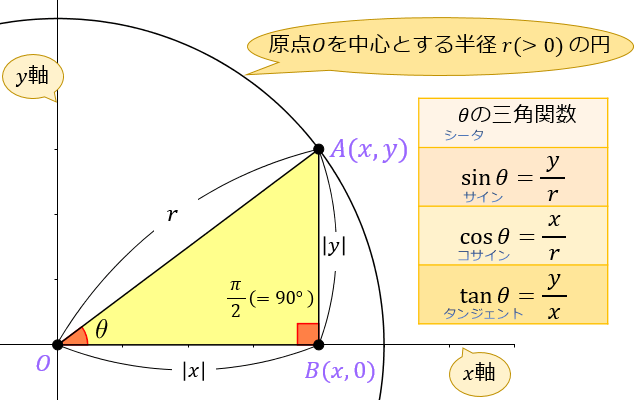
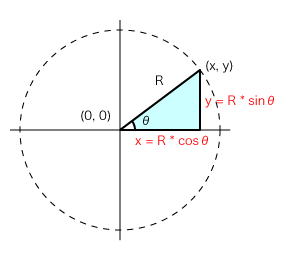
三角関数の具体的な使い方 正弦 (sin)・余弦 (cos)を使うことで斜辺の長さとその角度から幅と高さを得ることができます。 この計算式は地形の測量・ベクトルの座標計算・ゲームキャラクターの移動など様々な場面で活用できます。 x = cosΘ × h y = sinΘ × h まず、原点 O を中心とする 半径 r の円 と、その円上の 点 A (x, y) を考えます。 「 x 軸の正の部分」と線分 O A による(反時計回りを正とする)角の大きさ ∠ B O A = θ に対して 1 三角関数の角度の求め方、三角方程式の解き方 2 三角関数の角度を求めるsin編 21 三角関数の角度sinを求める①:単位円を利用する 22 三角関数の角度sinを求める②:sinθ=aのときy=aをグラフに書く
三角関数の定義のポイントは、 cos、sinは円のX座標、Y座標であるということです。 x軸の正の向きからθの角度をつけた直線を書くと円と交わりますよね。 この時のx,y座標がcosθ,sinθなのです。 半径1の単位円上の座標ということを考えると という範囲の制限があることも直感的に頷けますよね。のとき、sinΘ、cosΘ、tanΘの値を求めなさい。 まず、 弧度法 による角の表し方が理解できているかを確認してください。 弧度法では、" 180°=π "と表しました。 先ほど、 三角関数を考えるときに円の半径rの値に関係ない と書きました。 これは裏を返す角度にθ[°]を使用した場合、三角関数を用いて以下のような関係式が成り立ちます。 三角関数のtanθ=高さ/底辺 で求めることができるため、 タンジェントの逆関数であるtan1 を使用するとθ=tan1 (高さ/底辺)と計算できるのです。
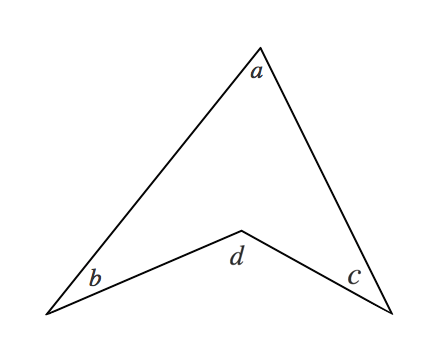



図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に



3
T riangle using Heron ′ s formula (1) S =√s(s−a)(s−b)(s−c), s = (abc) 2 (2) if a≥b,c h = 2S a, B=sin−1 h c, C= sin−1 h b if b≥ c,a h = 2S b, C =sin−1 h a, A=sin−1 h c if c≥ a,b h = 2S c, A= sin−1 h b, B=sin−1 h a (3) ABC = 180 T r i a n g l e u s i n g H e r o n ′ s f o r m u l a ( 1) S = s ( s − a) ( s − b) ( s − c), s = ( a b c) 2 ( 2)先生のいってることは分かったけど、でも、それは単にa,bの見方を変えただけで、角度θとの深い関係はやっぱり見えないと思うんですけど。 後はコサインが右辺の となる角度を求めて、60°±45°より、15°,105 三角関数の合成公式もその典型的象徴 こんにちは。 da Vinch (@mathsouko_vinch)です。 三角関数においてある角度の三角比を「覚える」のはナンセンスです。なぜなら三角関数では角度はいくらでも大きく、またマイナスの角度も考えられますから。さらに私たちがち




高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト




直角三角形の角度の求めかたは 直角三角形の残りの角度を求める 数学 教えて Goo
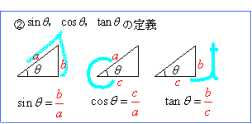
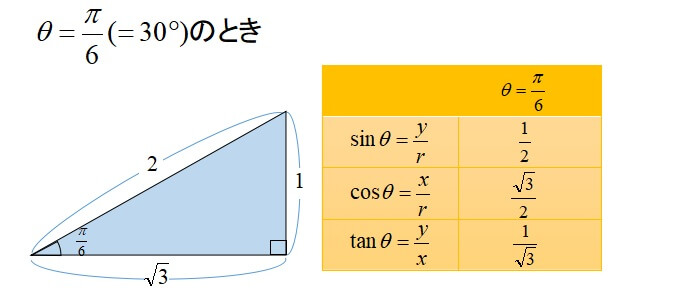
解説 ≪三角比の値の求め方≫ sinθ,cosθ,tanθの値は,次の「よく出る2つの三角形」と「sinθ,cosθ,tanθの定義」を覚えていれば導けます。 これらを使った求め方 ①θの値(角度)を見て,「よく出る2つの三角形」のうち,当てはまる三角形をかき出す。三角関数は周期関数なので、逆関数は多価関数である。 逆関数の性質から以下が成り立つ: =,() = / /ピタゴラスの定理 ピタゴラスの定理やオイラーの公式などから以下の基本的な関係が導ける 。 = ここで sin 2 θ は (sin(θ)) 2 を意味する。 この式を変形して、以下の式が導かれる:サインから角度を計算する方法 asin関数 を使用すると、サインから角度を計算することができます。 サインは、直角三角形の斜辺に対する対辺の比のことで、「対辺の長さ÷斜辺の長さ」になります。



三角関数 度 高精度計算サイト




角度の求め方 角度の求め方 Mqttk
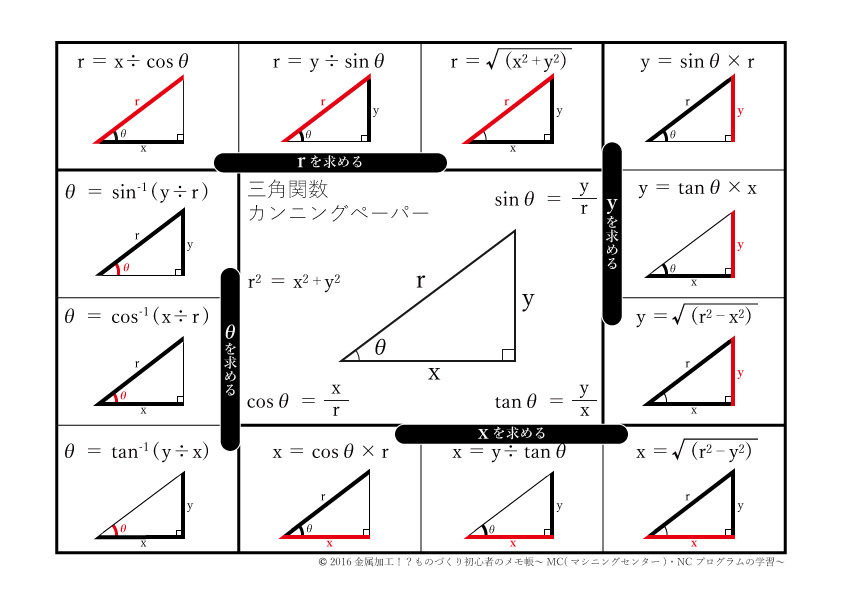
図1の直角三角形において、角 =30°が先にわかっている場合を考えます。 角 =30°ですから、3つの辺の比は1:2: になり、θ の向かい側の辺が対辺=1、 θに接する辺が底辺= がわかります。 このことを三角関数の tanを使って表すとtan30°= となります。 基本的に、三角関数の角度は 半径 \(1\) の「単位円」 を利用して求めることができます。 単位円 \(1\) 周分の角度は、度数なら \(\color{red}{360^\circ}\)、ラジアンなら \(\color{red}{2\pi}\) 直角三角形も、単位円も書かない方法なので、時短したいときなどにご活用ください(*˙꒳˙*)‧⁺ ︎* 目次 1、cos、sinの求め方 2、tanの求め方 ⌒⌒⌒⌒⌒⌒ * 必要なもの * ・左手 ・√(指の数) / 2 (こちらは頭の片隅に置いといてください♪
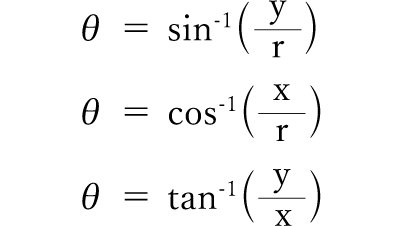



三角関数をマスターしよう その3 金属加工 ものづくり初心者のメモ帳 Mc マシニングセンター Ncプログラムの学習
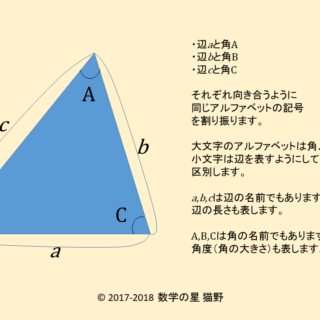



第2余弦定理の公式は辺と角度の関係を簡潔に表す 数学の星
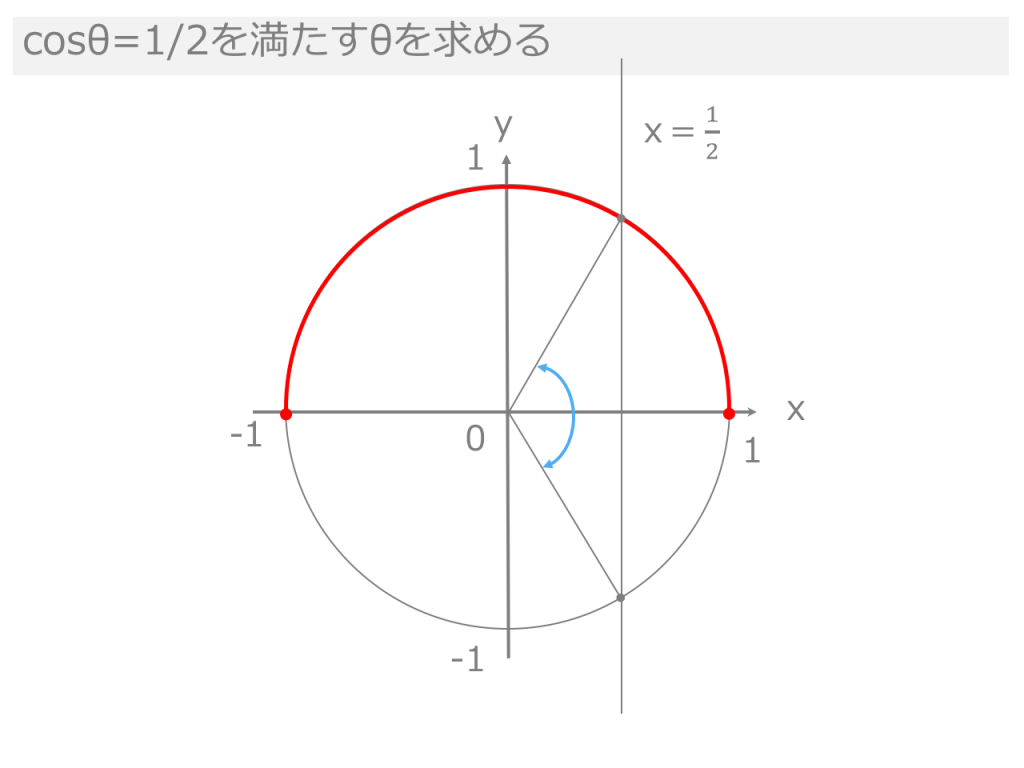
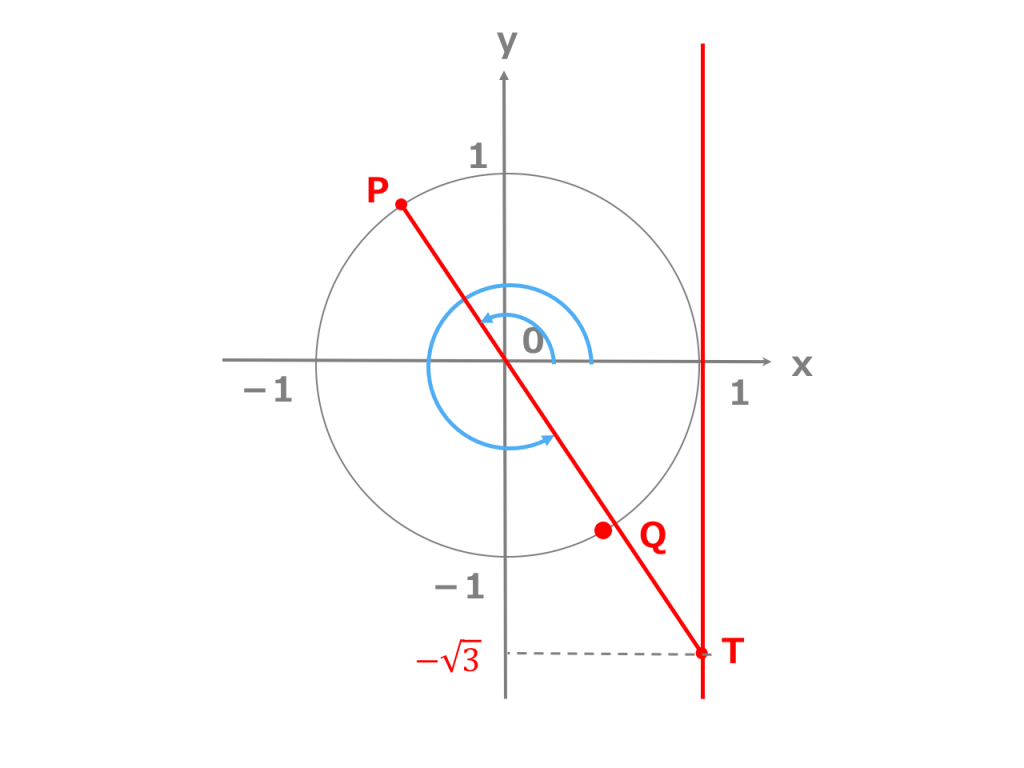
三角形の角度 無料で使える中学学習プリント 三角関数の基礎角度の求め方とは? (sinθ=1/2からθを計算 三角形の面積の求め方まとめ。 タイプ別でわかる公式一覧 三角形の面積は「 \ (底辺×高さ÷2\) 」という公式から求まりますが、この公式以外 三角関数の基礎では、角度を求めるということをよく行います。 今回は、その角度の求め方についての記事です。 例えば、 などといった問題があります。 「代表的な角度(30°、45°、60°など)のsin , cos , tanの値は暗記してるよ」 という人もいるかも< 鈍角の三角比1 > 角度θが90 以上の場合の三角比を 次で定める。 正の数r に対し,点Q(r,0) を原点 O(0,0) を中心として反時計まわりに角 度θだけ回転した点をP(X,Y) とする。 このとき角度θにおける三角比を sinθ= Y r, cosθ= X r, tanθ= Y X で定める。




三角形の辺や角が与えられたとき残りの辺や角を求める方法 数学の偏差値を上げて合格を目指す



三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典
関数電卓を使って三角関数の計算をするやり方をやさしく解説します。 関数電卓の角度設定 前回 Pythonを使った偏差値の求め方① 点数リストをファイルから読み込んで偏差値を計算しよう 前回は点数リストがプログラムの中に書かれていましたが・三角関数から角度(逆三角関数) 三角関数から角度(逆三角関数)を計算します。 sin(サイン)から角度 cos(コサイン)から角度 0 はじめに 三角関数について思うこと 三角関数というと高校時代に苦しだ方も多いかもしれません。とにかく公式も多くて、最初のうちは何に使えるのかよくわからない印象を抱きがちです。しかし実際は、理系であればいかなる分野に




高校数学 直角三角形を用いた三角比 Sin8 Cos8 Tan8 の定義とその理由 30 45 60 の三角比 受験の月



三角関数 1 Cg 数学 06aa
高さと斜辺から角度と底辺を計算 直角三角形の高さと斜辺から傾斜角と底辺を計算します。 三角形の3辺から角度を計算 三角形の3辺の長さから3角の角度を計算します。正弦定理を理解するために前提となる事柄 1 「正弦」とは三角関数のうちの sin θ の値のことで、正弦定理を使うためには 0 °~ 180 ° の三角関数の値が言えなければなりません。 実際に、宙で暗記して言えなければならなのは次の9つの値だけです。角度 θ (525度は 525、5度12分6秒は 5'12'6 と入力) 6桁 10桁 14桁 18桁 22桁 26桁 30桁 34桁 38桁 42桁 46桁 50桁 斜辺 c 高さ b Right triangle cosθ= a c , sinθ = b c ,



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ



Q Tbn And9gcq7h6dlzvq5e0plulfvxu64dpvadasyky0sizoi2drjv Uyz1m5 Usqp Cau
三角形の3辺の長さから角度を求める 三角形の記号 使用する記号ですが、図のように、三辺の長さを\( a,b,c \)、角度を\(A,B,C\)で表すことにします。 角度は、次の2段階のステップで求めます。 求める角度の余弦(cos(コサイン))を求める。




三角関数の基礎知識



Windows電卓で三角関数を計算する方法 Trismegistuslabo トリメギブログ



角度の求め方 算数の教え上手 学びの場 Com




三角関数は何に使えるのか サイン コサイン タンジェントの活躍 Qiita



三角形とは 面積公式 角度 辺の長さ 重心 比の計算 受験辞典




三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ




角度の場合分けについて 数学 苦手解決q A 進研ゼミ高校講座




小5 算数 小5 31 三角形の角 Youtube




高校数学 三角比 三角比を使った三角形の面積の求め方 Sin Cos ヘロンの公式を使った方法 数学の面白いこと 役に立つことをまとめたサイト



三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ




三角形の3辺から角度を計算 高精度計算サイト



直角三角形の角度の求め方 教えて下さい 斜辺以外の2辺の長さが分かっ Yahoo 知恵袋




角度の求め方 算数の教え上手 学びの場 Com



Excelで三角関数の計算 Acos関数を使ってみよう パソコンスキルと資格のscワンポイント講座



角度 の 求め 方 ニュース ニュース




余弦定理で角度を求める方法 数学の星



三角比と三角関数 高校物理をあきらめる前に 高校物理をあきらめる前に



Sin Cos Tanの値の覚え方 数学 苦手解決q A 進研ゼミ高校講座




三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com
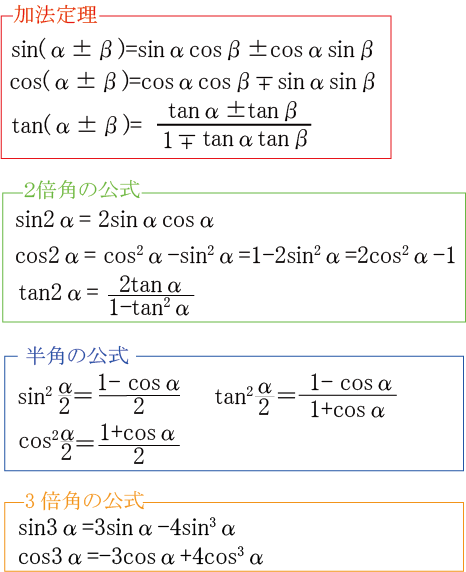



三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com



三角関数の合成とは 公式 証明 最大最小や範囲の問題 受験辞典



1




三角関数の知識 やさしい電気回路
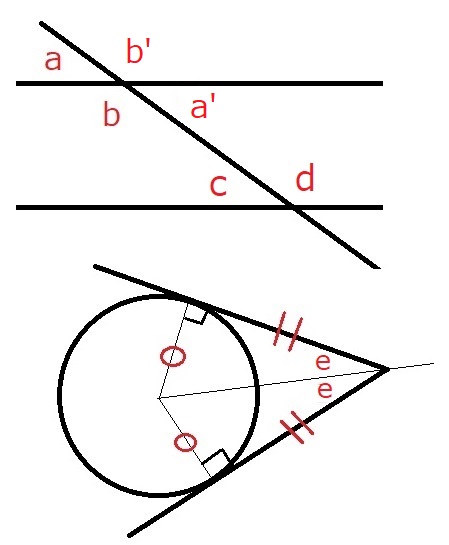



三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ




Excel 三角形の角度を底辺や斜辺 高さから求める方法 直角三角形の角度の計算
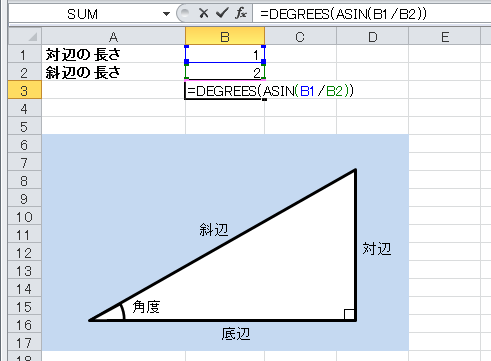



サインから角度を計算するには Asin Degreesの解説 エクセル関数リファレンス
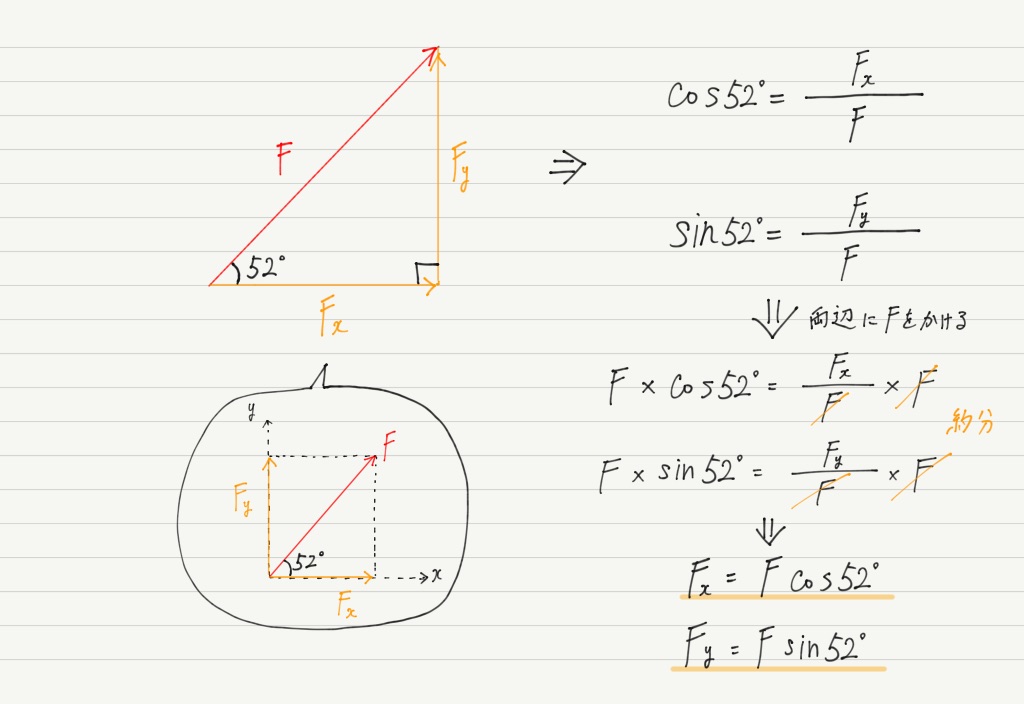



力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に
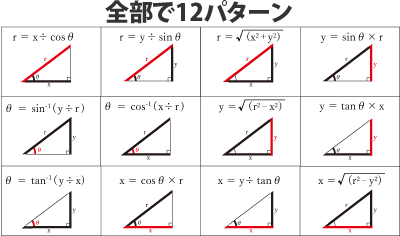



三角関数をマスターしよう その2 金属加工 ものづくり初心者のメモ帳 Mc マシニングセンター Ncプログラムの学習



直角三角形ではない場合ピタゴラスの定理はどう使えるのでしょうか Quora




角度の求め方 算数の教え上手 学びの場 Com




三角形の角度を求める問題 小学生 中学生の勉強




三角関数で角度から座標を導くふたつの式の使い途 Qiita



2点間の距離を測ろう 三角関数 Gameworks Lab
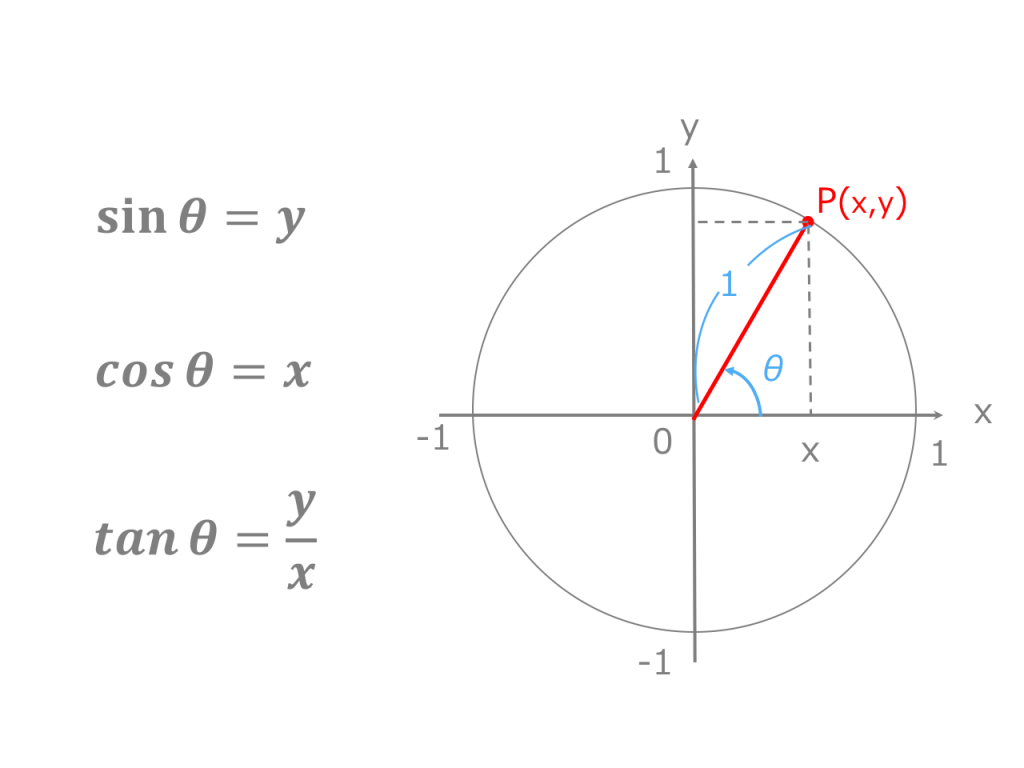



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ
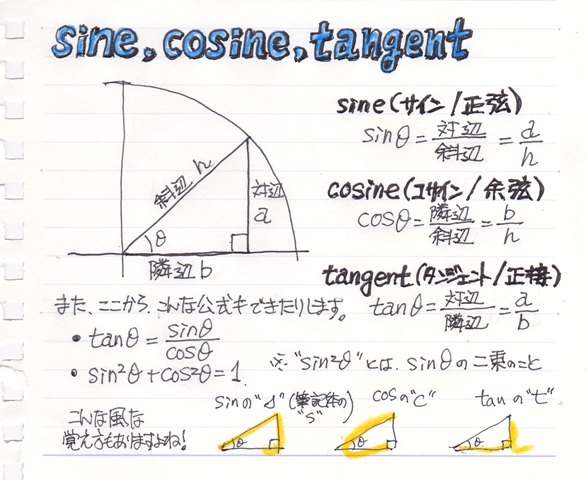



三角関数で直角三角形の辺の比率を求めてみた サイン コサイン タンジェントとか Excel 三角関数 Haku1569 Excel でらくらく データ分析
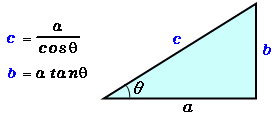



角度と底辺から斜辺と高さを計算 高精度計算サイト




直角三角形の底辺と高さで角度を求める 電卓で墨だし計算 Teacup ブログ Autopage




1研究中 C 数学1 三角関数 1 逆三角関数 三角比 ラジアン Sin Cos Tan Asin Acos Atan Atan2




三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ
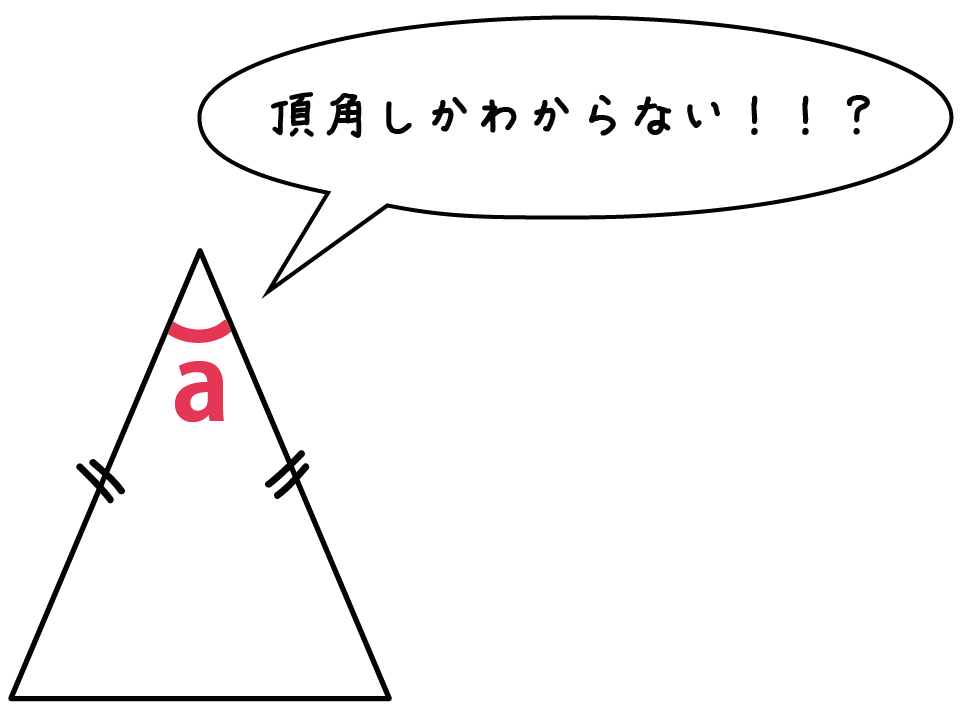



簡単公式 二等辺三角形の角度の2つの求め方 Qikeru 学びを楽しくわかりやすく




底辺と高さから角度と斜辺を計算 高精度計算サイト




Excel 三角関数と逆三角関数で 三角形の辺の長さや角度を求める方法まとめ わえなび ワード エクセル問題集
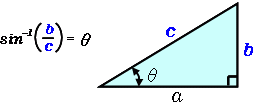



逆三角関数 度 高精度計算サイト




二等辺三角形の角を求める Youtube



上級 三角関数 Shade3d チュートリアル



三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ




タンジェントとは何か 中学生でも分かる三角関数の基礎



三角関数をマスターしよう その3 金属加工 ものづくり初心者のメモ帳 Mc マシニングセンター Ncプログラムの学習



三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com




高校数学 数 76 三角比 基本編 Youtube



サイン コサイン タンジェントの角度の求め方 一歩一歩ぐんぐんブログ




三角形の角度を求める問題 小学生 中学生の勉強
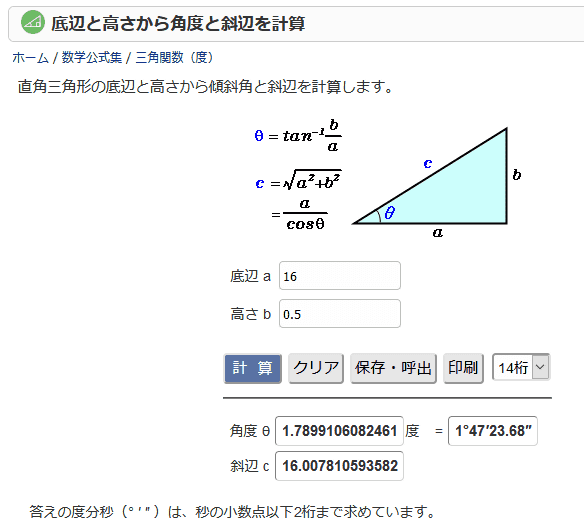



表計算ソフトを使って 底辺 と 高さ から 角度 を求める
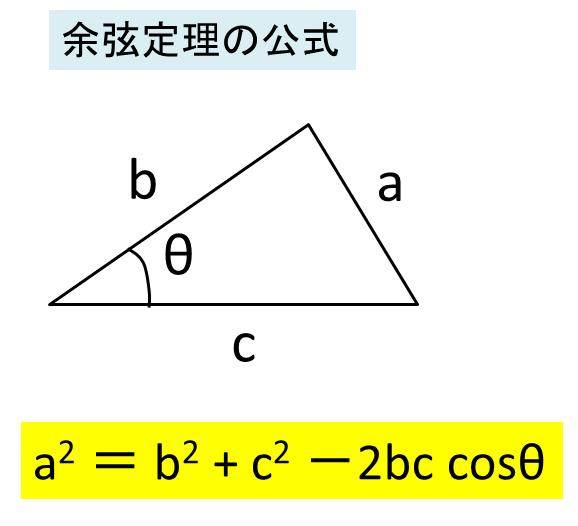



Excel エクセルで余弦定理の計算をする方法 角度や辺の長さを求める




直角三角形の辺を求める Youtube
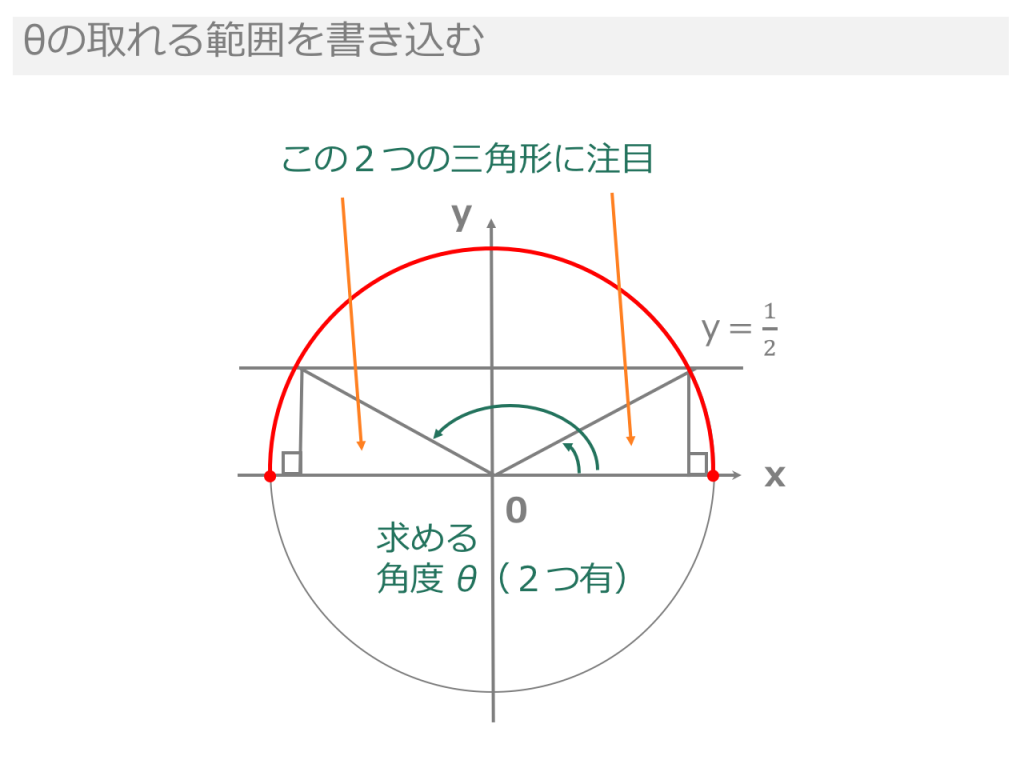



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ
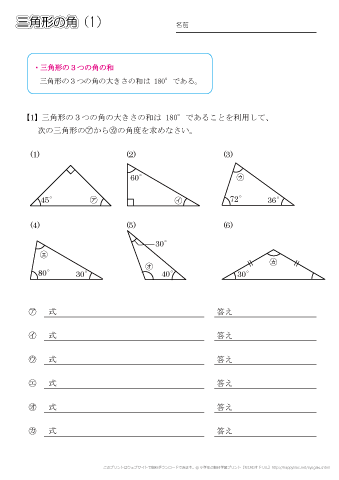



小学5年生の算数 多角形の角 三角形の角 問題プリント ちびむすドリル 小学生
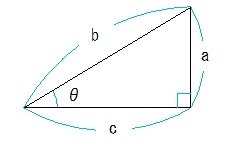



三角関数 ncプログラム基礎知識




Javaでmathクラスを使って三角関数を求める方法を現役エンジニアが解説 初心者向け Techacademyマガジン
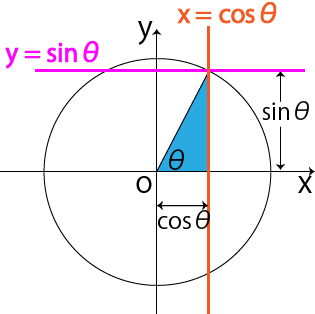



三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ




正弦定理から 三角形の辺の長さを求める計算について 数学 苦手解決q A 進研ゼミ高校講座



三角形の角度を求める 思考力を鍛える数学
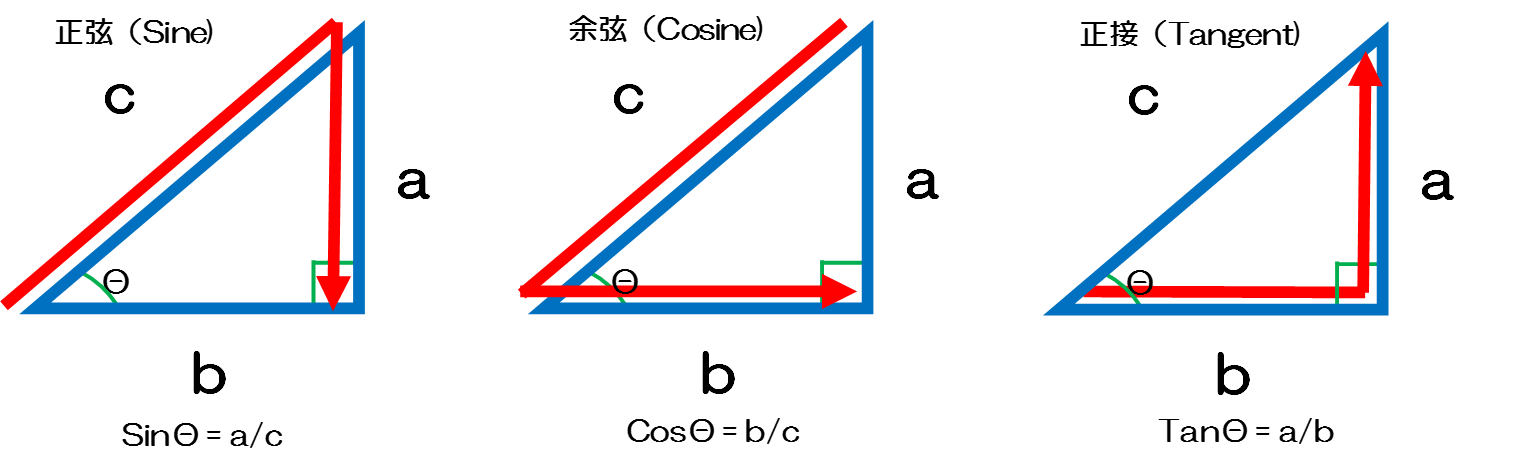



Vba 三角比をもとめる Sin関数 Cos関数 Tan関数 角度をもとめる Atn関数



三角関数から角度 逆三角関数 三角形の計算 計算サイト



3分でわかる 三角関数の角度の求め方 三角方程式を解く 合格サプリ
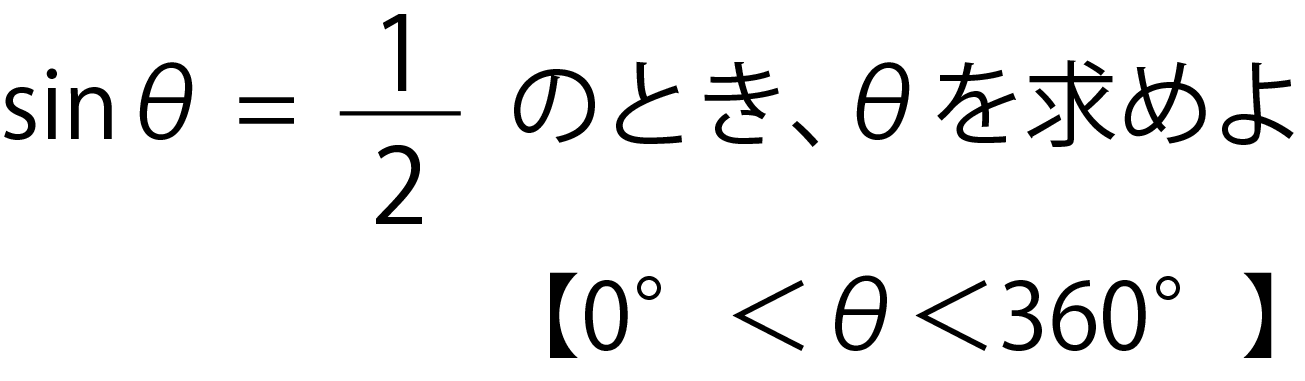



三角関数の基礎 角度の求め方とは Sin8 1 2から8を計算 高校生向け受験応援メディア 受験のミカタ



1



4 2 三角関数 Yasushi Noguchi Class
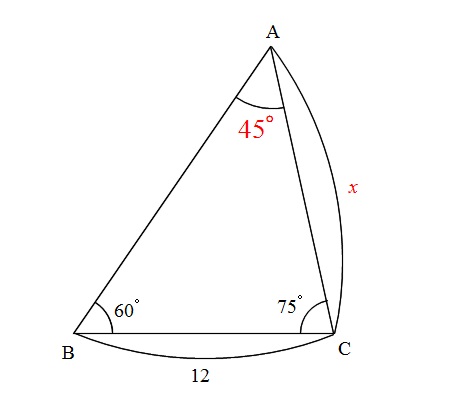



三角形で角度が2つ分かっているのに正弦定理も余弦定理も使えない



日曜大工で使う数式




タンジェントとは何か 中学生でも分かる三角関数の基礎
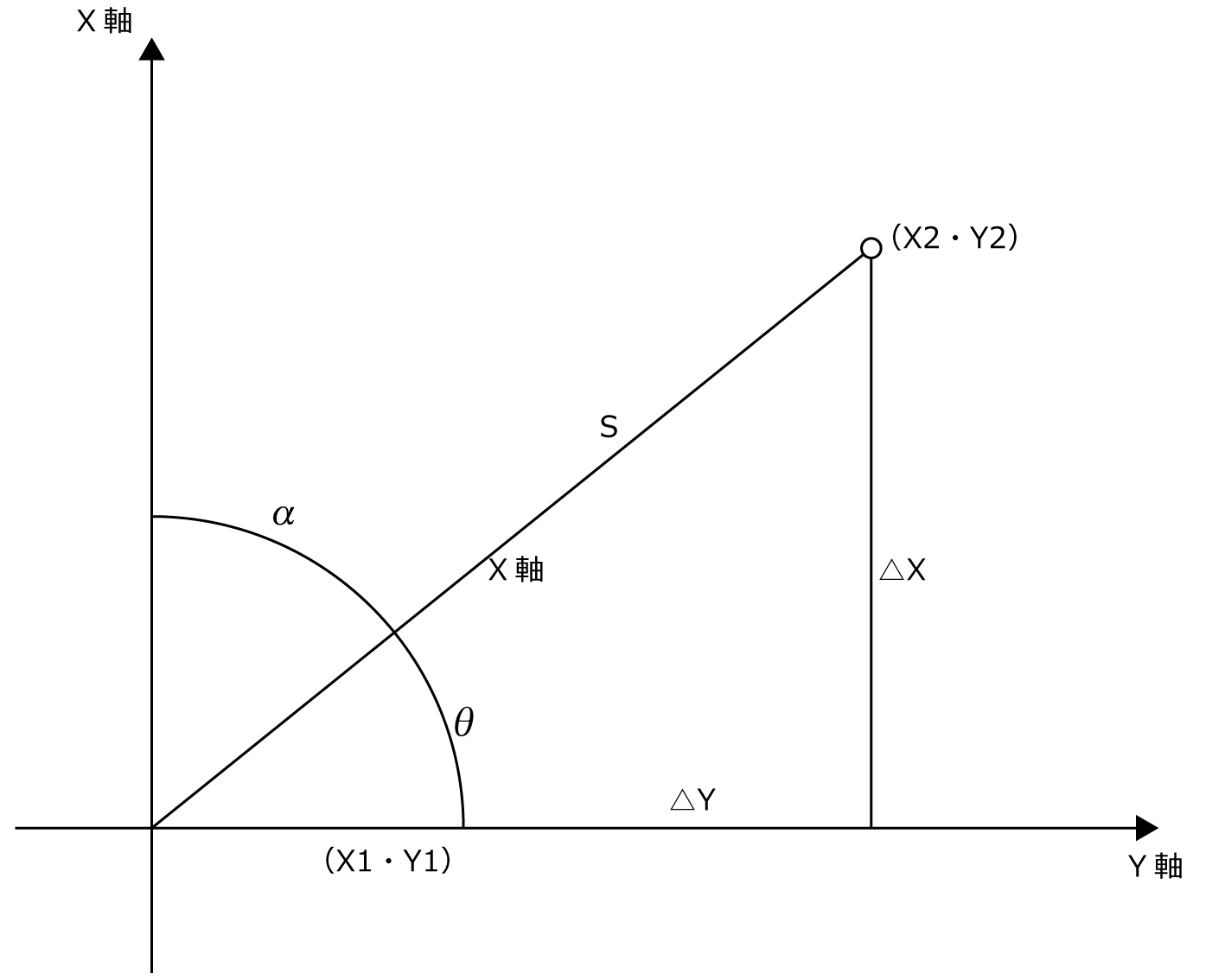



座標から角度の求め方 測量 測量機の情報ページ
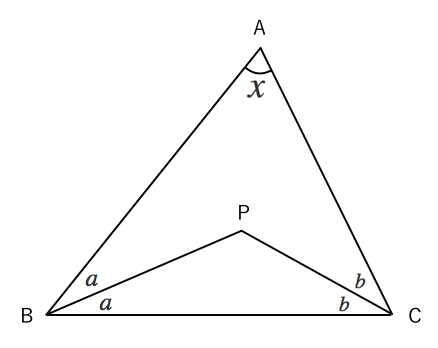



図形の調べ方 三角形 役に立つ角度の求め方 苦手な数学を簡単に




高校数学 三角比からの角度の求め方1 Sin8 映像授業のtry It トライイット




三角形の辺から角度を計算 製品設計知識
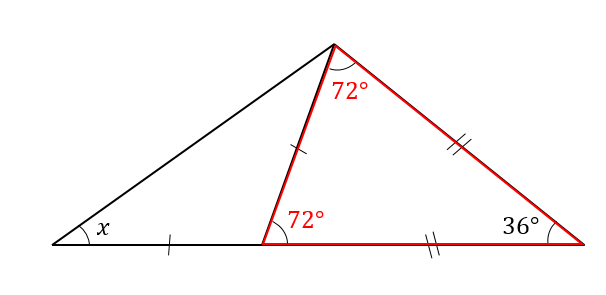



二等辺三角形の角度の求め方を問題を使って徹底解説 数スタ




中学数学 正三角形の角度の求め方がわかる3ステップ Qikeru 学びを楽しくわかりやすく



紙ヒコーキ型図形の角度を求める 平行線と角 勉強ナビゲーター



三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ



三角関数の角度は 3分でわかる求め方 公式と計算 表との関係




三角関数の合成公式 証明 問題 Cos型について 理系ラボ




高校数学 三角比からの角度の求め方3 Tan8 映像授業のtry It トライイット
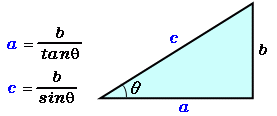



角度と高さから底辺と斜辺を計算 高精度計算サイト




三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ




余弦定理とは何か 図解でわかるその使い道と公式の証明 アタリマエ



三角関数の角度は 3分でわかる求め方 公式と計算 表との関係




三角形の面積の求め方まとめ タイプ別でわかる公式一覧 アタリマエ




三角関数は何に使えるのか サイン コサイン タンジェントの活躍 Qiita




高校数学 三角比からの角度の求め方1 Sin8 映像授業のtry It トライイット




力の分解 三角比編 高校物理をあきらめる前に 高校物理をあきらめる前に


コメント
コメントを投稿