Sin cos tan 公式 覚え方 178101

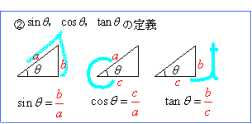
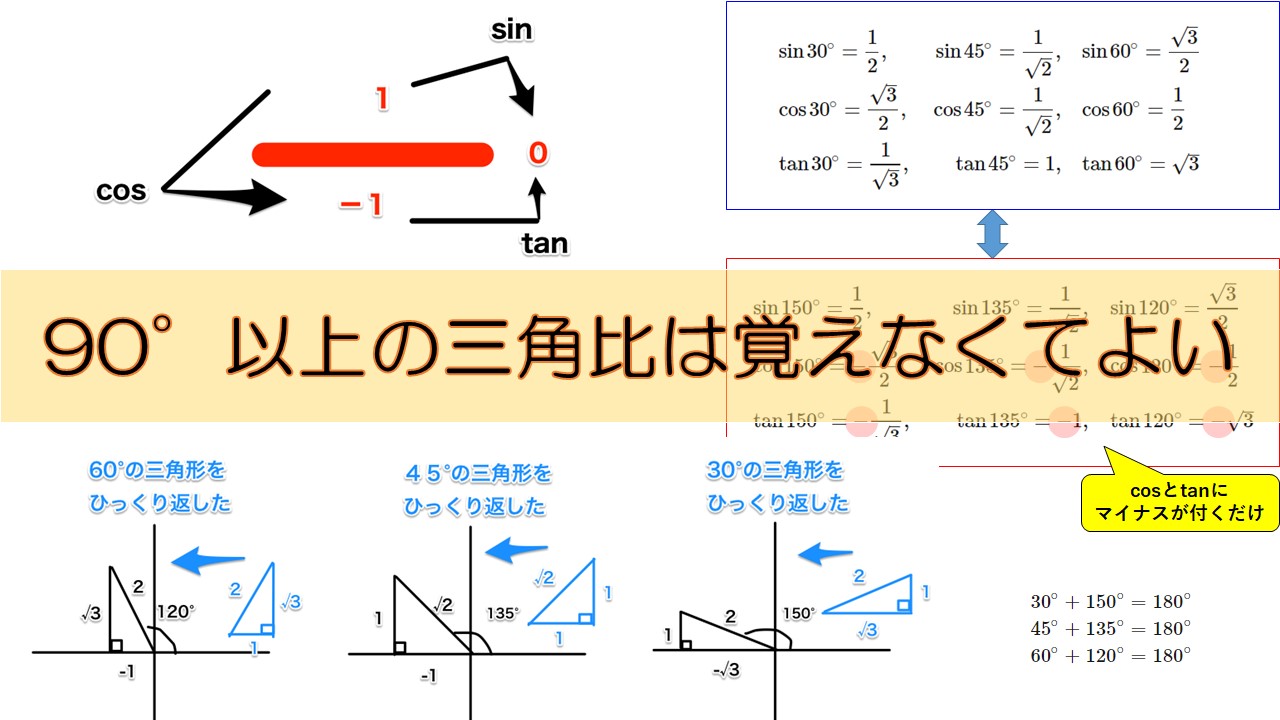
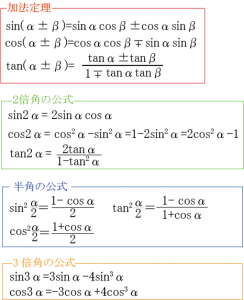
 → 印刷用pdf版は別頁 三角関数の加法定理，倍角公式，3倍角公式，半角公式 三角関数の和や積には多くの公式がありますが，「加法定理は覚える，他は作る」というのが，作者おすすめの考え方です。・・・ただし，そういう公式があるということと，およその形は記憶にとどめます。Sinθ，cosθ，tanθの値は，次の「よく出る2つの三角形」と「sinθ，cosθ，tanθの定義」を覚えていれば導けます。 これらを使った求め方 ①θの値（角度）を見て，「よく出る2つの三角形」のうち，当てはまる三角形をかき出す。 ②「sinθ，cosθ，tanθの定義」を三角形に当てはめて，辺の比を導く。 ただし，このように導くことがニガテな人は，次のように覚えてSin、cos、tanの三倍角の公式と証明、練習問題を用いて解説！ 三角関数の公式(sin,cos,tan)と覚え方 21年映像授業ランキング

三角関数の加法定理とその証明 おいしい数学

Sin cos tan 公式 覚え方

Sin cos tan 公式 覚え方-4 2倍角の公式を使う例題 41 例題1｜有名角でないサインコサインの値を求める; 全部覚えていれば楽だけど、第一象限のsinとtanだけ覚えておいて sin (90θ)=cosθ、cos (90°θ)=sinθ とか sin (θ180°)=sinθ とかの基本的な変換公式や加法定理などを覚えていれば何とかなります。 グラフの形を覚えておくのも大事ですね。

三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com

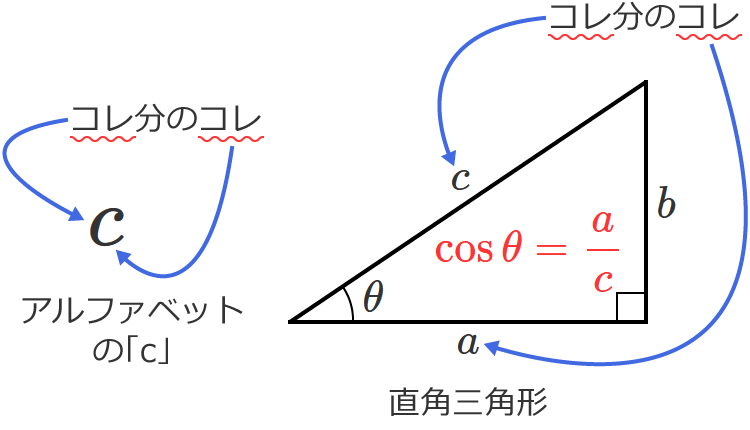
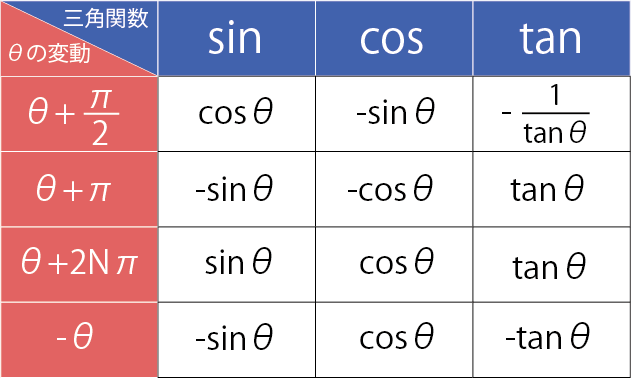
このテキストでは、数学Ⅰの三角比で使う公式を一覧にしています。 ＜目次＞ サイン・コサイン・タンジェントの求め方 sin・cos・tanの関係 90°－Aのときのsin・cos・tan 90°＋θのときのsin・cos・tan 180°－θのときのsin・cos・tan 正弦定理 余弦定理 直角三角形での三角比の覚え方とは、 直角が右下に来るように直角三角形を動かした後 、 筆記体「s」を当てはめることでsinを求め、 筆記体「c」を当てはめることでcosを求め、 筆記体「t」を当てはめることでtanを求める方法です。 実際に見ていき4 2倍角の公式を用いて変形します。 sinの3倍角の証明、cosの3倍角の証明 証明には加法定理と2倍角の公式を利用します。

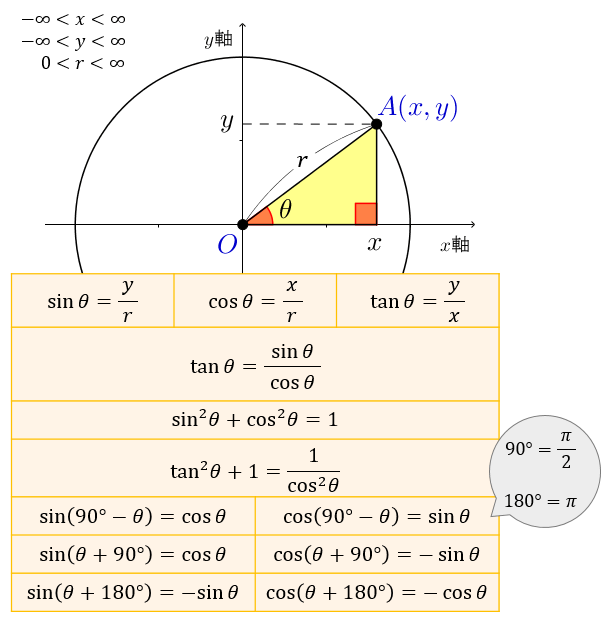
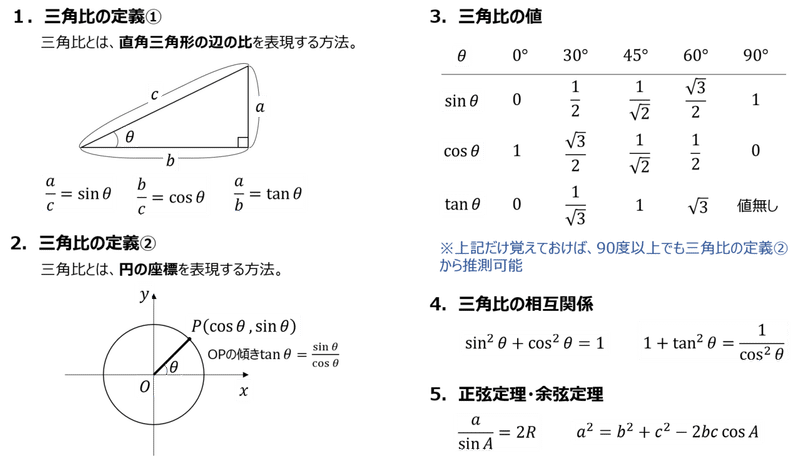
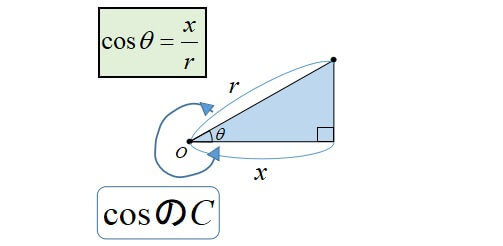
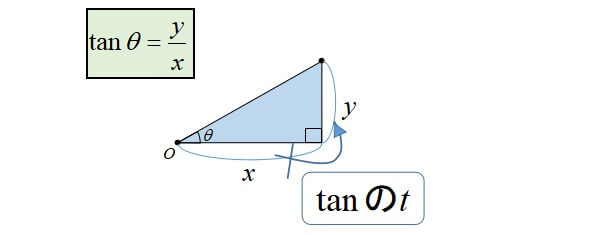
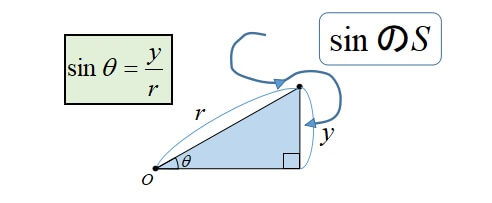
 三角比の相互関係から、\(\sin \theta\)、\(\cos \theta\)、\(\tan \theta\) のうち どれか \(1\) つでも値がわかれば、残りの \(2\) つの値を求められる のです！ 三角比の問題では必須の公式なので、すべて正確に覚えましょう。 三角比の相互関係の覚え方三角関数の周期性と対称性から得られる公式 三角関数には、周期性と対称性があります。この性質より、以下の関係式が得られます。 なお、周期性とは、角 θ の大きさに対して、関数（sin θ, cos θ, tan θ）の値が、一定の θ の間隔で繰り返されることを言います。 tanは an、と手を動かして書いてみれば、sin（θ）=Y/r、cos（θ）=X/rは、無理なく覚えられる。 cosの公式 cos（θ）=cos（θ） 図を書けば分かる公式なので、この公式も覚えない。

_____ tan=一个角的对边比邻边 sin=一个角的对边比斜边 cos=一个角的邻边比斜边 三角函数是数学中属于初等函数中的超越函数的一类函数它们的本质是任意角的集合与一个比值的集合的变量之间的映射通常的三角函数是在平面直角最後にtanの半角の公式ですが、これはsinとcosの半角の公式を使って求めていきます。 tanの半角の公式の証明 tan2 2 = sin2 2 cos2 2 三角関数の相互関係式tan = cos sin より = 1 cos 2 1cos 2 sinとcosの半角の公式をそれぞれ代入した = 1 cos 1 cos tanの半角の公式が導けた！Sin,cos,tan (180°−θ)の覚え方｜看護受験の必須 数学の公式を確認テスト vol38 Author看護予備校KAZアカデミー 第2回〆切まで 13 days 19 hrs 02 mins 48 secs それでは、本日も看護受験に必須の数学の公式を極めていきましょう。 sin (90°−θ),cos (90°−θ),tan (90°−θ

三角関数と指数対数の対策について 受験戦略の無敵超人 センター90 突破コース 早大完全合格コース

三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com

 公式として表すと次のとおりです。 tan x については、sin x と cos x の合成関数として考えることができるので省略します。 (1) (sin x)' = cos x (2) (cos x)' = sin x負角公式完成！ 「サインは出てくる コスると消える」 sin sin cos cos S C S C tan の公式群は，いずれも左の相互関係の公式から求められる。 まずはsin, cos をしっかり憶えよう。 tan , tan tan , tan tan1 2 tan2 三角比の公式 21 加法定理 (1) sin( ) = sin cos cos sin ⃝1 信_ 号_ そのまま_ 行_ 進_ OK (2) cos( ) = cos cos ∓sin sin ⃝1 こ_ こで _ 逆転_ シメ_ シメ_ (3) tan( ) = tan tan 1∓tan tan ＋の語呂合わせ タン_ プラ_ タン_;

数学 三角比 Sin Cos Tanの表と覚え方 理系ラボ

3倍角の公式の覚え方や証明は 入試問題付きでわかりやすく解説 東大医学部生の相談室

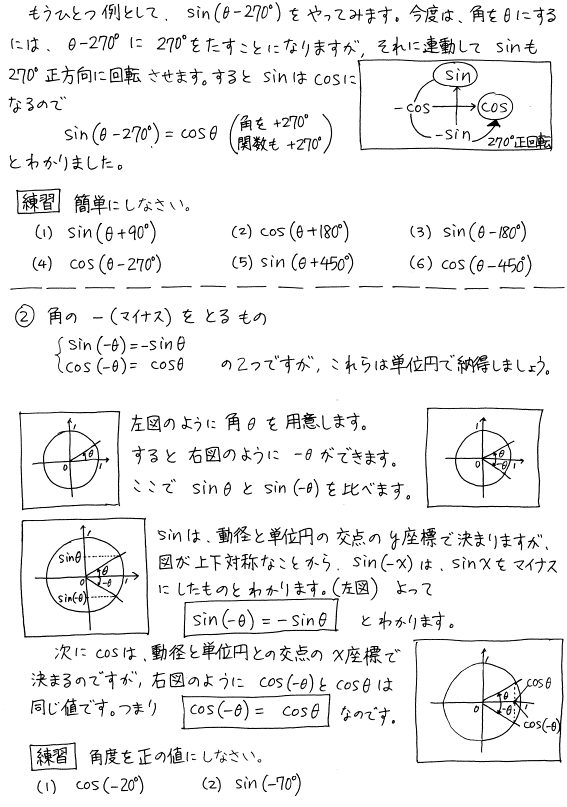
 sin ⁡ ( 18 0 ∘ θ) = − sin ⁡ θ \sin (180^ {\circ}\theta)=\sin\theta sin(180∘ θ) = −sinθ cos ⁡ ( 18 0 ∘ θ) = − cos ⁡ θ \cos (180^ {\circ}\theta)=\cos\theta cos(180∘ θ) = −cosθ tan ⁡ ( 18 0 ∘ θ) = tan ⁡ θ \tan (180^ {\circ}\theta)=\tan\theta tan(180∘ θ) = tanθ 〜 36 0 ∘ θ 2倍角の公式とその覚え方（語呂合わせ） 2倍角の公式 2倍角の公式は以下のようになっています。 cosθは3種類の公式があるのですが、どれも\(sin^2θcos^2θ=1\)を利用して展開しているだけなので、1つ覚えておけば十分です。 この公式を利用することで、 こんにちは、ウチダショウマです。 さて、角度 θ（シータ）に対し定義される"三角比"という値には、「サインコサインタンジェント（sin cos tan）」の $3$ 種類があります。 ふつうの定義と覚え方は図の通りです。 それぞれの 頭文字「s」「c」「t」の筆記体とリンクさせることで覚え

三角関数の還元公式 電気の神髄

三角関数に関する数値計算を伴う証明問題 身勝手な主張

 3倍角の公式 cos3θ = 4cos3θ − 3cosθ sin3θ = − 4sin3θ 3sinθ tan3θ = 3tanθ − tan3θ 1 − 3tan2θ このうち sinとcosの3倍角の公式は重要なので覚えておく必要がありますが非常に覚えづらい です。 そこで、語呂合わせによる3倍角の公式の覚え方を教えたいと思い 三角比・三角関数を攻略するためには、 sin・cos・tan（サイン・コサイン・タンジェント）の値を確実に求められるようになること が重要だ。 また、 有名角の三角比を自由自在に使えるようになること が特に重要なので、しっかりと学習してほしい。 さらに、相互関係の公式を利用して、三角比を求めていくことも三角比・三角関数の問題を解いていくために基本三角関数2｜偏角の変換公式は覚えるな！ 簡単に導く方法！ が成り立つことを説明しましたが，この三角比の角度の変換公式は三角関数でも同様に成り立ちます． ( 90 ∘ θ) などの変換公式も出てきます． これらの公式は非常に多いため，全部を

3

三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ

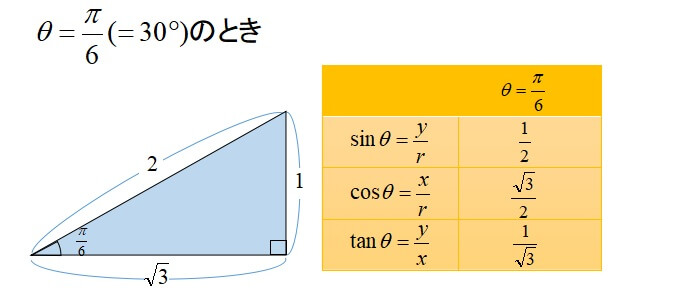
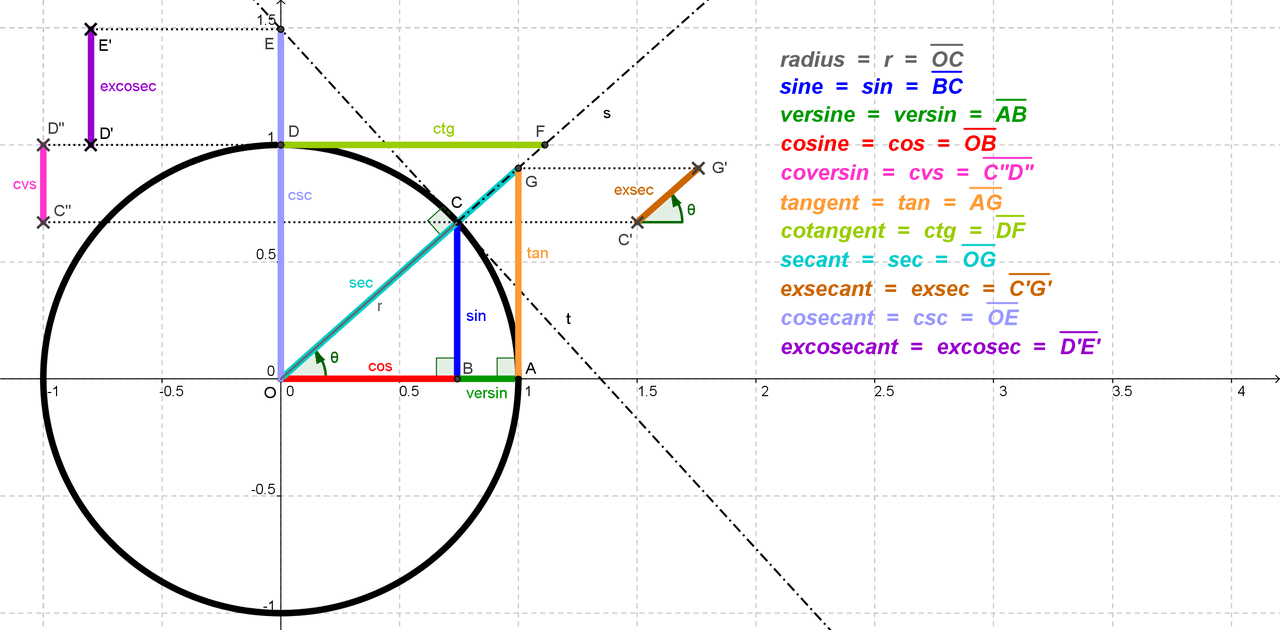
C o s e c x = 1 sin ⁡ x \mathrm {cosec} x=\dfrac {1} {\sin x} cosecx = sinx1 , cot ⁡ x = 1 tan ⁡ x \cot x=\dfrac {1} {\tan x} cotx = tanx1 c o s e c \mathrm {cosec} cosec のことを サイン・コサイン・タンジェント まず、原点 O を中心とする 半径 r の円 と、その円上の 点 A (x, y) を考えます。 「 x 軸の正の部分」と線分 O A による（反時計回りを正とする）角の大きさ ∠ B O A = θ に対して 全て覚えなければいけない超重要公式ですので、 暗記の手助けに活用してください！ 1 三角比の表 三角比の中でも、主な角の値を表でまとめます。 三角比の詳しい解説は 「数学Ⅰ三角比sin cos tanの表と覚え方」 の記事でまとめているので、ぜひ参考にしてください。 数学Ⅰ三角比sin cos tanの表と覚え方 0° 30°

三角関数についての質問です この表を覚えるコツってありますか 覚え Yahoo 知恵袋

3倍角の公式の覚え方をマスターしよう 高校生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

数学Ⅰ三角比sin cos tanの変換公式と覚え方 🤲 三角比は直角三角形で考える、三角関数は円で考えるのが基本です。 私が適当に作った問題ですが、 これしかわかっていない図形から、残りの辺の長さが全て出せるようになります。 本記事の「4：必ず覚えよう！sin・cos・tanの重要公式3つ」でも紹介した通り、tanθ=sinθ/cosθなので、sinθとcosθを求めてから、 tanθ =（12/13）/（5/13） = 12/5・・・（答） としてtanθを求めることもできます。 問題その2 cos 2 θ=25/29のとき、tanθの値を求めよ。 解答＆解説半角の公式の導き方 半角の公式は3つあります： sin2θ 2 = 1 − cosθ 2 cos2θ 2 = 1 cosθ 2 tan2θ 2 = 1 − cosθ 1 cosθ それぞれ証明してみましょう。 ただし、半角の公式を証明するためには、倍角の公式を理解しておく必要があります。 →2倍角の公式の証明と

半角の公式の使い方 導出 覚え方 具体例で学ぶ数学

三角関数講座その５ 不等式 簡単なグラフの問題 高校数学の知識庫

三角関数 公式 sin（πーθ) cos（πーθ) tan（πーθ)の覚え方 導き出し方Sin、cos、tanの三倍角の公式の2通りの証明 🤲 （応用）三倍角の公式の導き方 三倍角の公式も加法定理と二倍角の公式使うことで導き出せます。 これを上のcosの二倍角の公式に代入していきます。 15 半角公式のもう一つの導き方 重要!3倍角の公式と覚え方 sinとcosは語呂合わせで覚えるのがいいと思います。 tanはあまり良い語呂合わせがないので頑張って覚えてください。 sinとcosはtanよりも使う機会が多いような気がします。難関大学受験者は必ず3つとも覚えておきましょう。

三角関数の公式の一覧 Wikipedia

三角関数の公式 Sin Cos Tan と覚え方

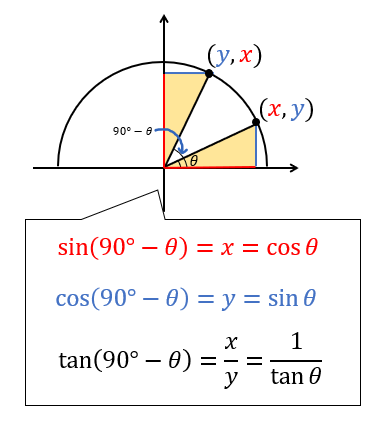
3 2倍角の公式の証明 31 2倍角の公式｜\(\sin2\theta\)の変形;1_まい_ タン_ タン_ 211 半角公式$$\cos (90°\theta)=\sin\theta$$ $$\tan (90°\theta)=\frac{1}{\tan\theta}$$ となっていることが分かりますね！ よって 90ｰθの変形を忘れてしまった場合には、このように直角三角形を書いて見比べてみると思い出すことができますね(^^) 三角比 90θの覚え方！

三角比は1時間で解けるようになる 箕輪 旭 Note

三角関数のsin Cos Tanって何

Tan と cot の周期 2π の移動 sin, cos, csc, sec の周期 の式を一般化する場合分母に21が出てくるため、単位として度よりもラジアンを使用した方がよい。 sinの3倍角の公式を加法定理で変形すると ※sin、cos、tanについてもっと深く学習したい人は、 sin・cos・tanについて詳しく解説した記事 をご覧ください。 覚えかた付きですごく分かりやすいのですが一つ問題があります。 数Ⅱバージョン 数Ⅱでは、円を用いて定義します。

三角関数の性質 公式の覚え方 おときち副塾長 電脳空間学習塾かもん Youtube

三角比 180 8 90 8 90 8の公式の覚え方と使い方をイチから 数スタ

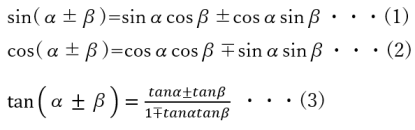
三角関数 加法定理およびその他の派生公式の覚え方 高校生 数学 公式 家庭教師のアルファ プロ講師による高品質指導

サインコサインタンジェント Sin Cos Tan とは何を表す 良い覚え方を紹介 遊ぶ数学

三角関数 還元公式の覚え方

Sin Cos Tan 三角比 三角関数の基礎をスタサプ講師がわかりやすく解説 ガジェット通信 Getnews

半角 二倍角の公式の覚え方は 覚えない事 その重要な意味と方法

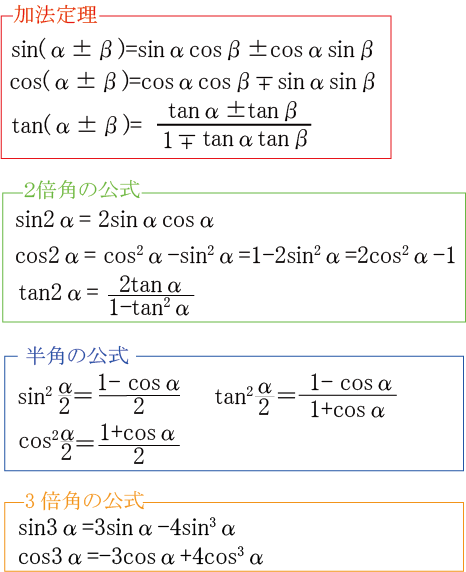
加法定理とは 公式と証明 簡単な覚え方を語呂合わせで説明します 高校生向け受験応援メディア 受験のミカタ

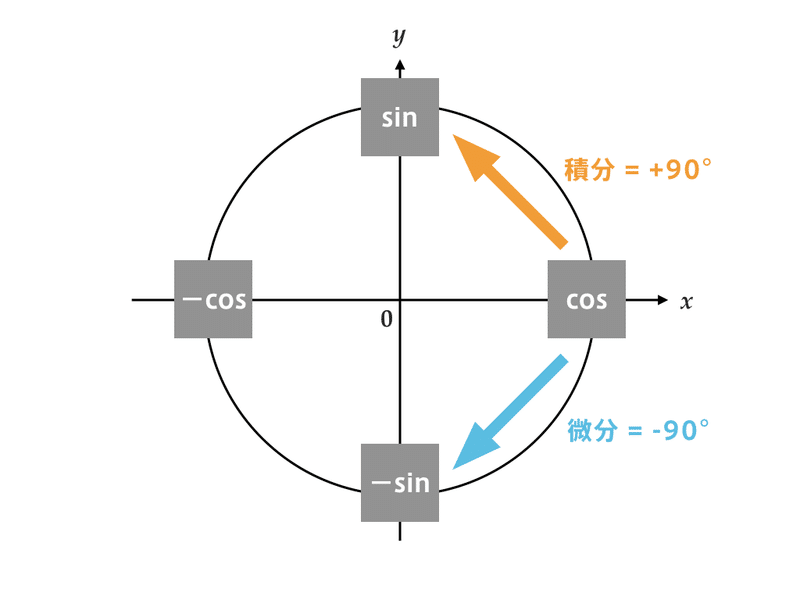
三角関数の微分 積分の覚え方 関谷 翔 Note

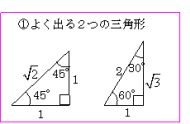
Sin Cos Tanの値の覚え方 数学 苦手解決q A 進研ゼミ高校講座

3

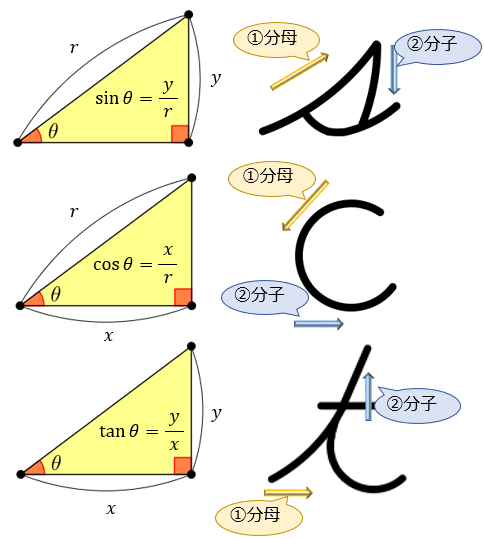
三角関数の基礎知識 Sin8 Cos8 Tan8 の覚え方 弧度法 三角比の表まとめ アタリマエ

三角比の表 三角関数表 Sin Cos Tan の値 の一覧 受験辞典

三角関数の公式 Sin Cos Tan と覚え方

Sin Cos Tan 180 8 の覚え方 看護受験の必須 数学の公式を確認テスト Vol38 Kazアカデミー 大阪の看護学校 看護予備校

三角関数講座その２ 合成と方程式 最大値 高校数学の知識庫

三角関数 還元公式の覚え方

三角関数の性質の覚え方ってありますか とてもじゃないほど覚えきれません Clear

余弦定理の覚え方 語呂合わせやイメージで暗記しよう 数学の面白いこと 役に立つことをまとめたサイト

Sin Cos Tan 公式覚え方 三角比 三角関數の基礎sin Cos Tanが簡単に分かる解 Gkgnae

数学2 三角関数 高校数学の難関 三角関数の重要ポイントがわかります

高校数学 三角関数の相互関係を用いる証明 映像授業のtry It トライイット

三角関数の角度の求め方や変換公式 計算問題も徹底解説 受験辞典

三角関数の公式 Sin Cos Tan と覚え方

48s96ub7b0z5f Net Sankakukansuu Koushiki

三角比 三角関数の基礎sin Cos Tanが簡単に分かる解説 Rikeinvest

三角関数の公式の覚え方と導出のコツ一覧 丸暗記不要

三角関数とは 三角関数の基礎 試験にでる要点まとめ 高校生向け受験応援メディア 受験のミカタ

3倍角の公式の導出と覚え方 おいしい数学

三角関数 加法定理 時習館 ゼミナール 高等部

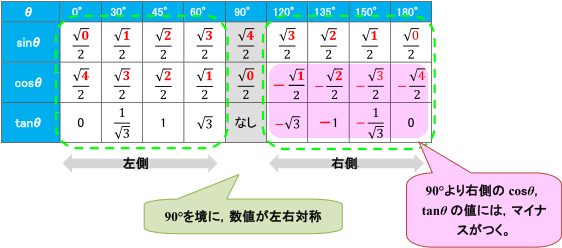
Sin Cos Tanの値の覚え方 数学 苦手解決q A 進研ゼミ高校講座

三角関数の加法定理とその証明 おいしい数学

Sin Cos Tanの値の覚え方 数学 苦手解決q A 進研ゼミ高校講座

高校数学 三角比 三角比の求め方と覚え方 Sin Cos Tan 数学の面白いこと 役に立つことをまとめたサイト

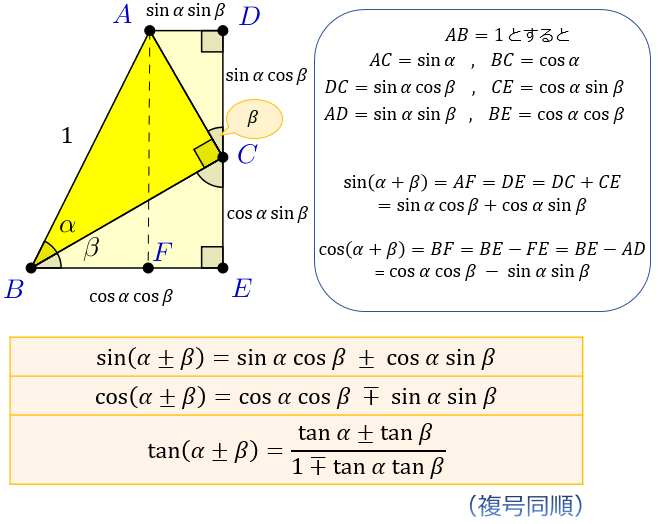
三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ

この公式がまったく覚えられないのですが良い覚え方ないですか Clear

わかりやすい三角比と基本公式 Irohabook

有名角の三角関数は覚えるな 図から簡単に判断するコツ

半角の公式の使い方 導出 覚え方 具体例で学ぶ数学

三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com

3分で分かる 2倍角の公式の覚え方と証明 使い方をわかりやすく 合格サプリ

3

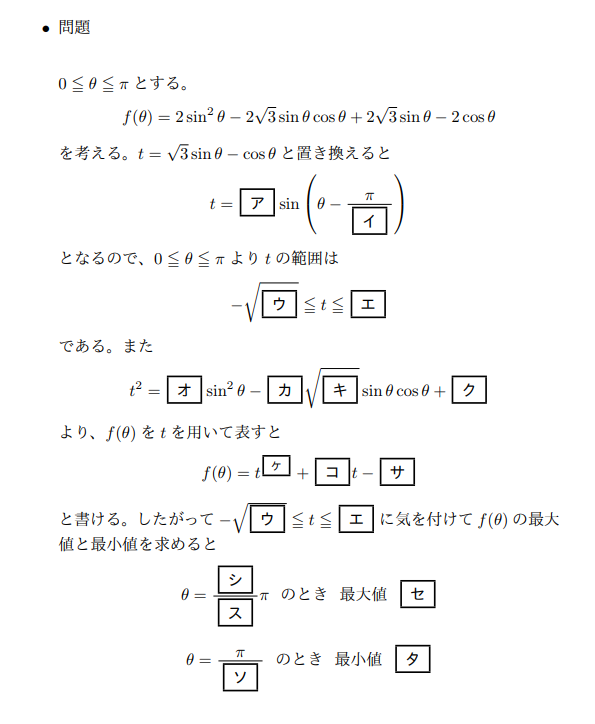
三角関数講座その３ 置き換え 2次関数 高校数学の知識庫

2倍角の公式と半角の公式 おいしい数学

二倍角の公式の覚え方 語呂合わせ 即覚えられる 高校生向け受験応援メディア 受験のミカタ

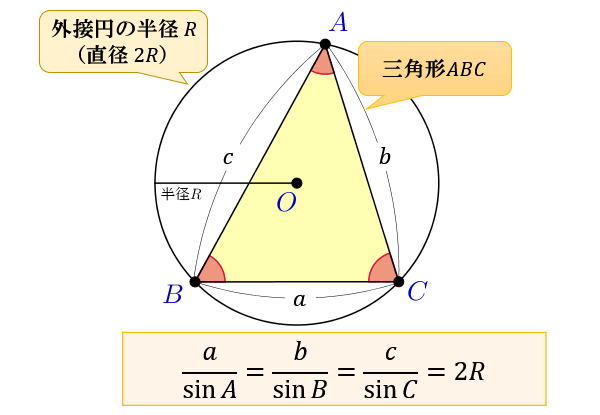
三角比 三角関数の公式一覧 正弦 余弦 加法定理など アタリマエ

2

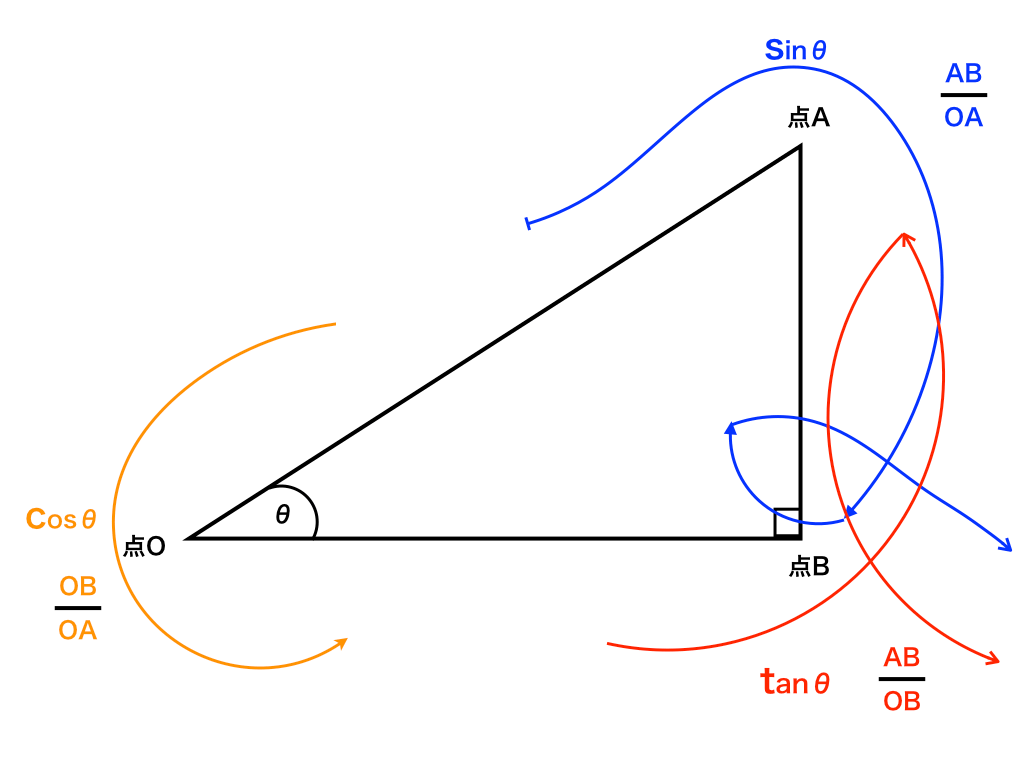
三角関数の公式の覚え方と導出のコツ一覧 丸暗記不要

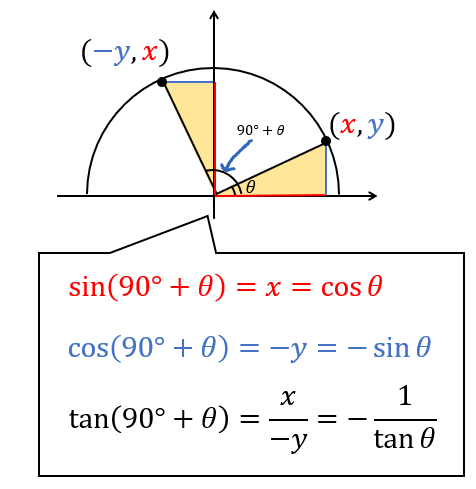
三角比 180 8 90 8 90 8の公式の覚え方と使い方をイチから 数スタ

三角関数の公式の覚え方と導出のコツ一覧 丸暗記不要

三角関数 機械加工でよく使う計算方法を説明します セドヤのブログ

三角関数 の基本的な定理とその有用性を再確認してみませんか その２ 加法定理 二倍角 三倍角 半角の公式等 ニッセイ基礎研究所

三角関数の性質って 全て暗記しなければいけないのでしょうか Yahoo 知恵袋

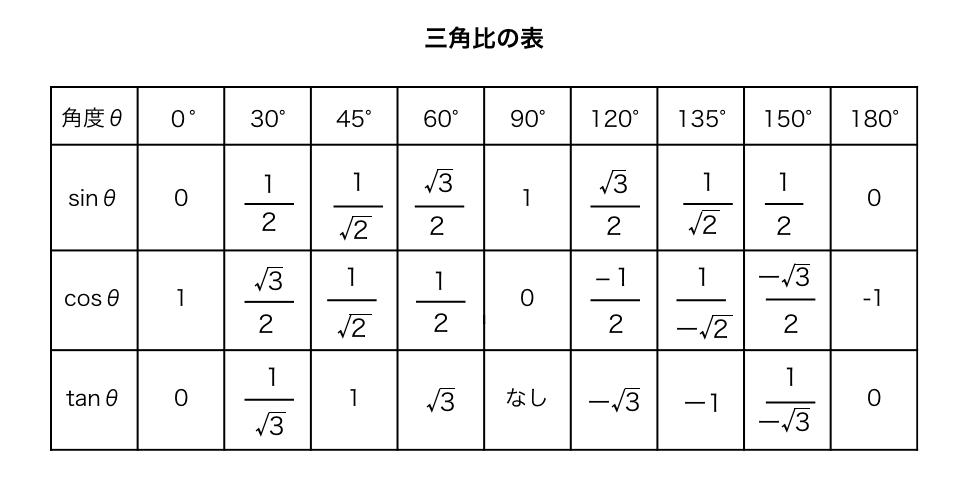
三角関数の公式 Sin Cos Tan と覚え方

三角比の表の値 Sincostan の覚え方を解説 単位円でマイナスも定義 遊ぶ数学

三角関数の公式の覚え方と導出のコツ一覧 丸暗記不要

高校数学 三角比 三角比の拡張 90 より大きいsin Cos Tanは簡単に求めることができる 数学の面白いこと 役に立つことをまとめたサイト

和積公式の語呂合わせ 怜悧玲瓏 高校数学を天空から俯瞰する

数学 三角比 Sin Cos Tanの公式まとめ 表 変換 相互関係 面積 正弦定理 余弦定理 理系ラボ

半角の公式 の効率的な覚え方と 証明 使える場面 次数を調整したい 青春マスマティック

サインコサインタンジェント Sin Cos Tan とは何を表す 良い覚え方を紹介 遊ぶ数学

一夜漬け高校数学7 三角比 覚え方 サイン コサイン タンジェント Youtube

三角関数の知識 やさしい電気回路

三角関数の公式 Sin Cos Tan と覚え方

数学 三角比 Sin Cos Tanの表と覚え方 理系ラボ

8をマスター 三角関数の加法定理 倍角と半角の公式 定額個別指導塾の櫻学舎 仙台五橋 家での勉強が1時間未満の子の為の学習塾

3

三角比 サイン コサイン タンジェント とは 定義と相互関係 受験辞典

Sin Cos Tan 高校生 数学のノート Clear

三角関数の知識 やさしい電気回路

三角比の公式まとめ サイン コサイン タンジェント 正弦定理 余弦定理など Irohabook

たった6つの公式から三角関数の公式を全て導く方法 塾講師ステーション情報局

加法定理の覚え方 図形でわかる公式の考え方 アタリマエ

数学 三角比 Sin Cos Tanの公式まとめ 表 変換 相互関係 面積 正弦定理 余弦定理 理系ラボ

三角関数の重要公式 加法定理の語呂合わせ 覚え方まとめ 合格サプリ

三角関数の公式覚え方sin Cos Tan M君

三角関数のsin Cos Tanとは 図解ですぐわかる 超重要な公式と練習問題も 高校生向け受験応援メディア 受験のミカタ

数学 三角比 Sin Cos Tanの表と覚え方 理系ラボ

三角関数は2時間で解けるようになる 外資系コンサルタントが主夫になったら

3分で分かる 三角関数の積和 和積の公式の覚え方 証明 使いどころをわかりやすく 合格サプリ

三角 関数 公式 三角関数の角度の求め方を公式や計算問題を通して徹底解説 Amp Petmd Com

3倍角の公式の覚え方や証明は 入試問題付きでわかりやすく解説 東大医学部生の相談室

三角比 サイン コサイン タンジェント とは 定義と相互関係 受験辞典

3分で分かる 三角関数の積和 和積の公式の覚え方 証明 使いどころをわかりやすく 合格サプリ

高2 数学ii B 三角比 三角関数公式まとめ 高校生 数学のノート Clear

加法定理とは 公式と証明 簡単な覚え方を語呂合わせで説明します 高校生向け受験応援メディア 受験のミカタ

三角比 180 8 90 8 90 8の公式の覚え方と使い方をイチから 数スタ

数学ii 怜悧玲瓏 高校数学を天空から俯瞰する